kmer: an R package for fast alignment-free clustering of biological sequences

Fri, Jul 6, 2018 clustering, sequence analysis

Introduction

Agglomerative clustering methods that rely on a multiple sequence alignment and a matrix of pairwise distances can be computationally infeasible for large DNA and amino acid datasets. Alternative k-mer based clustering methods involve enumerating all k-letter words in a sequence through a sliding window of length k. The *n* × 4^k matrix of k-mer counts (where n is the number of sequences) can then be used in place of a multiple sequence alignment to calculate distances and/or build a phylogenetic tree. kmer is an R package for clustering large sequence datasets using fast alignment-free k-mer counting. This can be achieved with or without a multiple sequence alignment, and with or without a matrix of pairwise distances. These functions are detailed below with examples of their utility.

Distance matrix computation

The function kcount is used to enumerate all k-mers within a sequence or set of sequences, by sliding a window of length k along each sequence and counting the number of times each k-mer appears (for example, the 4³ = 64 possible DNA 3-mers: AAA, AAC, AAG, …, TTT). The kdistance function can then compute an alignment-free distance matrix, using a matrix of k-mer counts to derive the pairwise distances. The default distance metric used by kdistance is the k-mer (k-tuple) distance measure outlined in Edgar (2004). For two DNA sequences a and b, the fractional common k-mer count over the 4^k possible words of length k is calculated as: $$F = \sum\limits_{\tau}\frac{min (n_a(\tau), n_b (\tau))}{min (L_a , L_b ) - k + 1} \tag{1}$$

where τ represents each possible k-mer, n_a(τ) and n_b(τ) are the number of times τ appears in each sequence, k is the k-mer length and L is the sequence length. The pairwise distance between a and b is then calculated as:

$$d = \frac{log(0.1 + F) - log(1.1)}{log(0.1)} \tag{2}$$

For n sequences, the kdistance operation has time and memory complexity O(n²) and thus can become computationally infeasible when the sequence set is large (e.g. > 10,000 sequences). As such, the kmer package also offers the function mbed, that only computes the distances from each sequence to a smaller (or equal) sized subset of ‘seed’ sequences (Blackshields et al., 2010). The default behavior of the mbed function is to select *t* = (*log*₂n)² seeds by clustering the sequences (k-means algorithm with *k* = t), and selecting one representative sequence from each cluster.

DNA and amino acid sequences can be passed to kcount, kdistance and mbed either as a list of non-aligned sequences or a matrix of aligned sequences, preferably in either the “DNAbin” or “AAbin” raw-byte format (see the ape package documentation for more information on these S3 classes). Character sequences are supported; however ambiguity codes may not be recognized or treated appropriately, since raw ambiguities are counted according to their underlying residue frequencies (e.g. the 5-mer “ACRGT” would contribute 0.5 to the tally for “ACAGT” and 0.5 to that of “ACGGT”). This excludes the ambiguity code “N”, which is ignored.

Example 1: Compute k-mer distance matrices for the woodmouse dataset

The ape R package (Paradis et al., 2004) contains a dataset of 15 aligned mitochondrial cytochrome b gene DNA sequences from the woodmouse Apodemus sylvaticus, originally published in Michaux et al. (2003). While the kmer distance functions do not require sequences to be aligned, this example will enable us to compare the performance of the k-mer distances with the alignment-dependent distances produced by ape::dist.dna. First, load the dataset and view the first few rows and columns as follows:

data(woodmouse, package = "ape")
ape::as.character.DNAbin(woodmouse[1:5, 1:5])
#>         [,1] [,2] [,3] [,4] [,5]
#> No305   "n"  "t"  "t"  "c"  "g" 
#> No304   "a"  "t"  "t"  "c"  "g" 
#> No306   "a"  "t"  "t"  "c"  "g" 
#> No0906S "a"  "t"  "t"  "c"  "g" 
#> No0908S "a"  "t"  "t"  "c"  "g"

This is a semi-global (‘glocal’) alignment featuring some incomplete sequences, with unknown characters represented by the ambiguity code “n” (e.g. No305). To avoid artificially inflating the distances between these partial sequences and the others, we first trim the gappy ends by subsetting the global alignment (note that the ape function dist.dna also removes columns with ambiguity codes prior to distance computation by default).

woodmouse <- woodmouse[, apply(woodmouse, 2, function(v) !any(v == 0xf0))]

The following code first computes the full *n* × n distance matrix, and then the embedded distances of each sequence to three randomly selected seed sequences. In both cases the k-mer size is set to 6.

### Compute the full distance matrix and print the first few rows and columns
library(kmer)
woodmouse.kdist <- kdistance(woodmouse, k = 6)
print(as.matrix(woodmouse.kdist)[1:7, 1:7], digits = 2)
#>         No305  No304  No306 No0906S No0908S No0909S No0910S
#> No305   0.000 0.0322 0.0295   0.033   0.036   0.037   0.037
#> No304   0.032 0.0000 0.0051   0.020   0.022   0.032   0.023
#> No306   0.030 0.0051 0.0000   0.016   0.017   0.026   0.018
#> No0906S 0.033 0.0202 0.0162   0.000   0.024   0.033   0.014
#> No0908S 0.036 0.0224 0.0171   0.024   0.000   0.033   0.025
#> No0909S 0.037 0.0322 0.0264   0.033   0.033   0.000   0.034
#> No0910S 0.037 0.0233 0.0176   0.014   0.025   0.034   0.000

### Compute and print the embedded distance matrix
set.seed(999)
seeds <- sample(1:15, size = 3)
woodmouse.mbed <- mbed(woodmouse, seeds = seeds, k = 6)
print(woodmouse.mbed[,], digits = 2)
#>         No0909S No0913S  No304
#> No305    0.0368  0.0391 0.0322
#> No304    0.0322  0.0102 0.0000
#> No306    0.0264  0.0098 0.0051
#> No0906S  0.0332  0.0215 0.0202
#> No0908S  0.0332  0.0273 0.0224
#> No0909S  0.0000  0.0368 0.0322
#> No0910S  0.0341  0.0176 0.0233
#> No0912S  0.0242  0.0322 0.0273
#> No0913S  0.0368  0.0000 0.0102
#> No1103S  0.0171  0.0251 0.0202
#> No1007S  0.0046  0.0368 0.0322
#> No1114S  0.0451  0.0428 0.0373
#> No1202S  0.0345  0.0176 0.0233
#> No1206S  0.0304  0.0251 0.0202
#> No1208S  0.0046  0.0409 0.0359

Example 2: Alignment-free tree-building

In this example the alignment-free k-mer distances calculated in Example 1 are compared with the Kimura (1980) distance metric as featured in the ape package examples. The resulting neighbor-joining trees are visualized using the tanglegram function from the dendextend package.

## compute pairwise distance matrices
dist1 <- ape::dist.dna(woodmouse, model = "K80") 
dist2 <- kdistance(woodmouse, k = 7) 

## build neighbor-joining trees
phy1 <- ape::nj(dist1)
phy2 <- ape::nj(dist2)

## rearrange trees in ladderized fashion
phy1 <- ape::ladderize(phy1)
phy2 <- ape::ladderize(phy2)

## convert phylo objects to dendrograms
dnd1 <- as.dendrogram(phy1)
dnd2 <- as.dendrogram(phy2)

## plot the tanglegram
dndlist <- dendextend::dendlist(dnd1, dnd2)
dendextend::tanglegram(dndlist, fast = TRUE, margin_inner = 5)

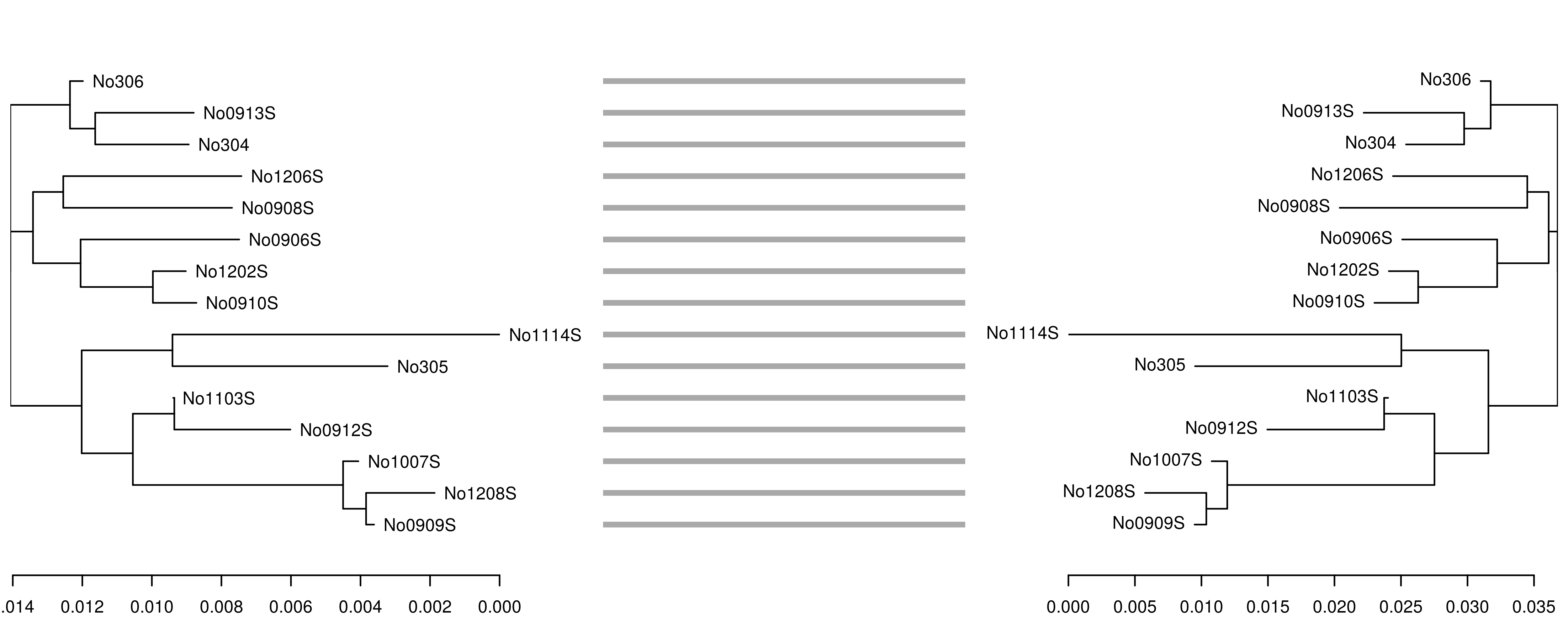
Figure 1: Tanglegram comparing distance measures for the woodmouse sequences. Neighbor-joining trees derived from the alignment-dependent (left) and alignment-free (right) distances show relatively congruent fine-scale topologies, with the exception of the single sequence No0908S.

Clustering without a distance matrix

To avoid excessive time and memory use when building large trees (e.g. n > 10,000), the kmer package features the function cluster for fast divisive clustering, free of both alignment and distance matrix computation. This function first generates a matrix of k-mer counts, and then recursively partitions the matrix row-wise using successive k-means clustering (k = 2). While this method may not necessarily reconstruct sufficiently accurate phylogenetic trees for taxonomic purposes, it offers a fast and efficient means of producing large trees for a variety of other applications such as tree-based sequence weighting (e.g. Gerstein et al. (1994)), guide trees for progressive multiple sequence alignment (e.g. Sievers et al. (2011)), and other recursive operations such as classification and regression tree (CART) learning.

The package also features the function otu for rapid clustering of sequences into operational taxonomic units based on a genetic distance (k-mer distance) threshold. This function performs a similar operation to cluster in that it recursively partitions a k-mer count matrix to assign sequences to groups. However, the top-down splitting only continues while the highest k-mer distance within each cluster is above a defined threshold value. Rather than returning a dendrogram, otu returns a named integer vector of cluster membership, with asterisks indicating the representative sequences within each cluster.

Example 3: OTU clustering with k-mers

In this final example, the woodmouse dataset is clustered into operational taxonomic units (OTUs) with a maximum within-cluster k-mer distance of 0.03 and with 20 random starts per k-means split (recommended for improved accuracy).

set.seed(999)
woodmouse.OTUs <- otu(woodmouse, k = 5, threshold = 0.97, method = "farthest", nstart = 20)
woodmouse.OTUs
#>   No305*    No304   No306*  No0906S  No0908S No0909S*  No0910S  No0912S 
#>        3        1        1        1        1        2        1        2 
#>  No0913S  No1103S  No1007S  No1114S  No1202S  No1206S  No1208S 
#>        1        2        2        3        1        1        2

The function outputs a named integer vector of OTU membership, with asterisks indicating the representative sequence from each cluster (i.e. the most “central” sequence). In this case, three distinct OTUs were found, with No305 and N01114S forming one cluster (3), No0909S, No0912S, No1103S, No1007S and No1208S forming another (2) and the remainder belonging to cluster 1 in concordance with the consensus topology of Figure 1.

Concluding remarks

The kmer package is released under the GPL-3 license. Please direct bug reports to the GitHub issues page at http://github.com/shaunpwilkinson/kmer/issues. Any feedback is greatly appreciated.

Acknowledgements

This software was developed with funding from a Rutherford Foundation Postdoctoral Research Fellowship from the Royal Society of New Zealand.

References

Blackshields,G. et al. (2010) Sequence embedding for fast construction of guide trees for multiple sequence alignment. Algorithms for Molecular Biology, 5, 21.

Edgar,R.C. (2004) Local homology recognition and distance measures in linear time using compressed amino acid alphabets. Nucleic Acids Research, 32, 380–385.

Gerstein,M. et al. (1994) Volume changes in protein evolution. Journal of Molecular Biology, 236, 1067–1078.

Kimura,M. (1980) A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. Journal of Molecular Evolution, 16, 111–120.

Michaux,J.R. et al. (2003) Mitochondrial phylogeography of the woodmouse (Apodemus sylvaticus) in the Western Palearctic region. Molecular Ecology, 12, 685–697.

Paradis,E. et al. (2004) APE: analyses of phylogenetics and evolution in R language. Bioinformatics, 20, 289–290.

Sievers,F. et al. (2011) Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Molecular Systems Biology, 7, 539.